Our research focuses on the mechanics of bacterial flagella. Bacteria propel themselves by rotating one or more helical slender structures, known as the flagella. The rotation generates a propulsive force that allows for the bacteria to locomote. At this length-scale, viscous forces overcome inertia, and the flow is at low Reynolds number.
Two primary challenges in modeling flagella include:
- Experimentally systematic manipulation of micron-sized bacterial flagella is difficult, and often impossible
- Numerically, coupling the hydrodynamics of the fluid with the structural mechanics of the flagella pose a challenging fluid-structure problem
To overcome these two challenges, we take a two pronged approach, and combine desktop model experiments and cutting-edge simulation tools from computer graphics.
Experiments: As an analog system for flagella, we consider custom fabricated flexible helical rods of ~20 cm length, and rotate them in a bath of glycerine, see the image below. Our procedure allows us to systematically vary all the relevant parameters: material (Young’s modulus), geometry (rod radius, helix pitch, helix radius, length of rod), and fluid (viscosity). The setup is temperature controlled since it allows us to change the viscosity of the fluid medium.
Figure: (a) Experimental apparatus: a helical rod (1), is rotated by a motor (2), inside a glycerin bath (3), that is enclosed by an external water tank (4) for temperature control. Two orthogonal video cameras (5,6) record the rod. (b) Schematic diagram of the rod.
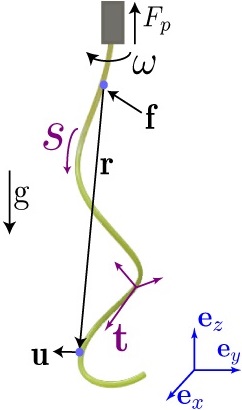Simulations: We performed numerical simulations where we combined Discrete Elastic Rods (DER) for an elastic description of the rod and Lighthill Slender Body Theory (LSBT) to model the hydrodynamics. DER describes a rod as a centerline parameterized by an arc-length parameter, s, and discretizes the line into a number of nodes. LSBT relates the velocity along the arc-length as a function of the viscous force applied by the fluid. Such a formulation accounts for the long-range hydrodynamic interaction between flows induced by distant parts of the rod. This is in contrast with Resistive Force Theories that use local drag coefficients, and can result in oversimplification.
Results: The flexibility of the flagellum interacts with the hydrodynamics to produce novel physical phenomena. Above a certain critical angular velocity, the hydrodynamic forces cause the rod to buckle (see video above). Our analysis shows that this buckling instability can potentially happen in biologically relevant regime. We hypothesize that natural bacteria exploit this instability for physiological purposes, e.g. to change swimming direction. For more details, please refer to our publications below.
Publications
- Jawed, M. K., Reis, P., “Dynamics of a flexible helical filament rotating in a viscous fluid near a rigid boundary” Physical Review Fluids 2:3, 034101 (2017)
- Jawed, M. K., Reis, P., “Deformation of a soft helical filament in an axial flow at low Reynolds number” Soft Matter 12, 1898-1905 (2016)
- Jawed, M. K., Khouri, N., Da, F., Grinspun, E., Reis, P., “Propulsion and instability of flexible helical rod rotating in viscous fluid” Physical Review Letters 115:16, 168101 (2015)
Press coverage: Physics Synopsis
Coauthors
Noor Khouri (MIT), Fang Da (Columbia), Eitan Grinspun (Columbia), Pedro Reis (MIT)
Image reused under Creative Commons Attribution-ShareAlike license (A. J. Cann, Flickr).